Hồi tiếp trạng thái là một phương pháp quan trọng trong điều khiển tự động và được sử dụng rộng rãi trong các ứng dụng thực tế. Đây là một phương pháp điều khiển tự động bằng cách sử dụng thông tin trạng thái được phản hồi về của hệ thống để tính toán, tạo ra tín hiệu điều khiển và áp dụng ngược lại các tín hiệu đó vào hệ thống. Việc hồi tiếp trạng thái giúp cải thiện hiệu suất, độ ổn định và chất lượng điều khiển theo mong muốn của hệ thống điều khiển.
1. Điều khiển hồi tiếp trạng thái
Cho đối tượng điều khiển mô tả bởi phương trình trạng thái:
\left\{ \begin{array}{l}
\dot x(t) = Ax(t) + Bu(t)\\
y(t) = Cx(t)
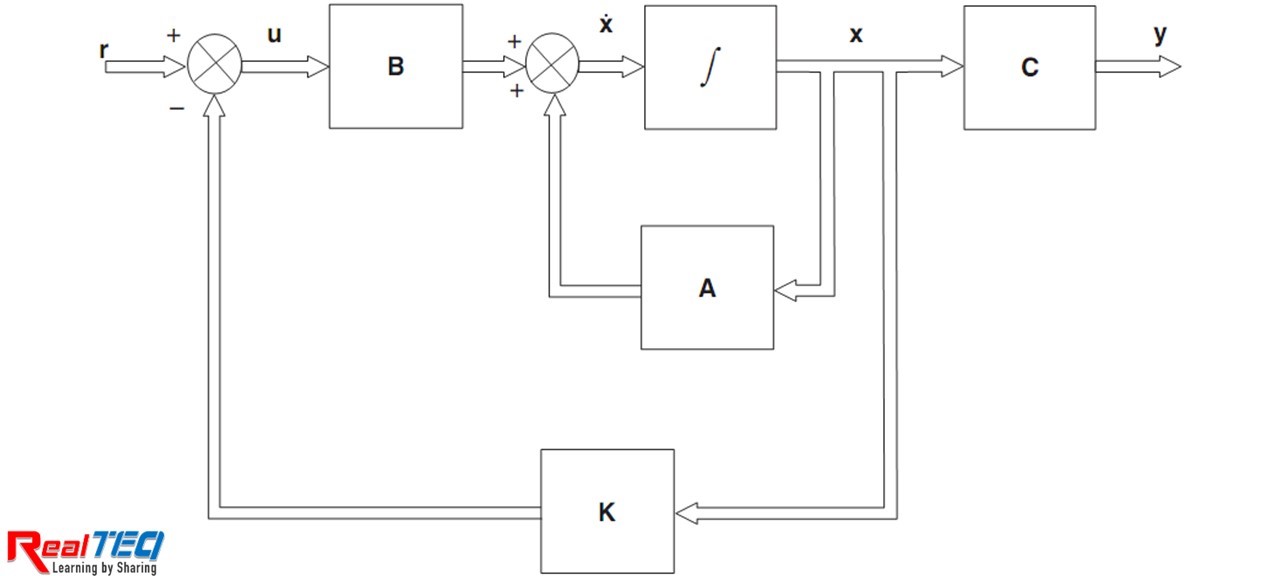
\end{array} \right. (1)Hình 1. Hệ thống điều khiển hồi tiếp trạng thái.
Hệ thống điều khiển đặt cực là hệ thống trong đó tín hiệu điều khiển được xác định bởi:
u\left( t \right) = r\left( t \right)-K.x\left( t \right)\ (2)
Trong đó:
- r: Vector trạng thái mong muốn.
- K: Ma trận hồi tiếp trạng thái.
Thay (2) vào (1) ta được:
\left\{ \begin{array}{l}
\dot x\left( t \right) = Ax\left( t \right) + B\left[ {r\left( t \right) - Kx\left( t \right)} \right]\\
y\left( t \right) = Cx\left( t \right)
\end{array} \right.Suy ra:
\left\{ \begin{array}{l}
\dot x\left( t \right) = \left[ {A - BK} \right].x\left( t \right) + B.r\left( t \right)\\
y\left( t \right) = C.x\left( t \right)
\end{array} \right.Dựa vào biến trạng thái x, ta có thể biết được theo thời gian thì hệ thống đang hoạt động như thế nào. Từ đó hồi tiếp về để so sánh với tín hiệu ngõ vào và xuất ra tín hiệu u điều khiển tác động vào hệ thống. Đây được gọi là điều khiển hồi tiếp trạng thái.
Mục đích của việc thiết kế hệ thống dùng phương pháp đặt cực là để cải thiện đáp ứng quá độ (giảm độ vọt lố, giảm thời gian quá độ), giúp cho hệ thống được ổn định và chất lượng điều khiển theo mong muốn.
Để có thể thiết kế được hệ thống hồi tiếp trạng thái, điều kiện cần là tất cá các trạng thái của hệ thống phải đo lường được (quan sát được) và hệ sẵn sàng nhận tín hiệu điều khiển (điều khiển được).
Khi không có ma trận hồi tiếp trạng thái K, tức là tín hiệu hồi tiếp về trực tiếp, thì có thể hệ thống đã ổn định nhưng chất lượng điều khiển hệ thống chưa đúng như mong muốn. Vì vậy, cần phải đặt vào khâu hồi tiếp một ma trận K và tính toán, thiết kế sao cho phù hợp để đảm bảo chất lượng điều khiển của hệ thống. Để xác định ma trận K, ta có thể sử dụng nhiều phương pháp như:
- Phương pháp đặt cực.
- Phương pháp LQR.
- Phương pháp PD…
2. Phương pháp đặt cực (phương pháp phân bố cực)
Phương pháp đặt cực là một trong những phương pháp để xác định ma trận hồi tiếp trạng thái K sao cho phương trình đặc tính có nghiệm tại vị trí mong muốn để đảm bảo chất lượng điều khiển của hệ thống.
Phương trình đặc tính của hệ hồi tiếp trạng thái là:
det\left[ {sI-A + BK} \right] = 0Có nhiều phương pháp để thiết kế bộ điều khiển phân bố cực, trong đó có ba cách chính thường được sử dụng như sau:
2.1. Phương pháp so sánh trực tiếp
Để thực hiện phương pháp này, ta làm theo các bước sau đây:
- Bước 01: Giả sử các cực vòng kín mong muốn:
s = {\mu _1},s = {\mu _2},....s = {\mu _n}- Bước 02: Đồng nhất hai vế ta tìm được ma trận K:
det \left| {sI - A + BK} \right| = \left( {s - {\mu _1}} \right)\left( {s - {\mu _2}} \right)...\left( {s - {\mu _n}} \right)Hay
\det \left| {sI - A + BK} \right| = {s^n} + {\alpha _1}{s^{n - 1}} + {\alpha _2}{s^{n - 2}} + ... + {\alpha _{n - 1}}s + {\alpha _n}Ví dụ 1: Cho đối tượng có hàm truyền sau, hãy xác định ma trận hồi tiếp trạng thái K sao cho phương trình đặc tính có nghiệm tại vị trí mong muốn để đảm bảo chất lượng điều khiển của hệ thống.
\frac{{Y\left( s \right)}}{{U\left( s \right)}} = \frac{1}{{{s^3} + 6{s^2} + 5s + 1}}Hướng dẫn:
Ta thành lập phương trình trạng thái dạng chính tắc điều khiển:
A=\left[\begin{matrix}0&1&0\\0&0&1\\-1&-5&-6\\\end{matrix}\right];B=\left[\begin{matrix}0\\0\\1\\\end{matrix}\right];C=\left[\begin{matrix}1&0&0\\\end{matrix}\right];D=0Chọn cặp cực phức và cực thứ ba cho hệ kín: -2± j.4; -10.
Phương trình đặc tính của hệ hồi tiếp trạng thái là:
det \left( {sI - A + Bk} \right) = \left( {s + 2 + j4} \right)\left( {s + 2 - j4} \right)\left( {s + 10} \right) = {s^3} + 14{s^2} + 60s + 200Suy ra:
det \left(s\left[\begin{matrix}1&0&0\\0&1&0\\0&0&1\\\end{matrix}\right]-\left[\begin{matrix}0&1&0\\0&0&1\\-1&-5&-6\\\end{matrix}\right]+\left[\begin{matrix}0\\0\\1\\\end{matrix}\right]\left[\begin{matrix}K_1&K_2&K_3\\\end{matrix}\right]\right)\\
=s^3+14s^2+60s+200\Leftrightarrow det\left(\left[\begin{matrix}s&-1&0\\0&s&-1\\1&5&s+6\\\end{matrix}\right]+\left[\begin{matrix}0&0&0\\0&0&0\\K_1&K_2&K_3\\\end{matrix}\right]\right)=s^3+14s^2+60s+200\Leftrightarrow det\left(\left[\begin{matrix}s&-1&0\\0&s&-1\\K_1+1&K_2+5&K_3+s+6\\\end{matrix}\right]\right)=s^3+14s^2+60s+200\Leftrightarrow s.s.\left(K_3+s+6\right)+K_1+1+\left(K_2+5\right).s=s^3+14s^2+60s+200
\Leftrightarrow s^3+K_3s^2+6s^2+\left(K_2+5\right)s+K_1+1=s^3+14s^2+60s+200
Cân bằng hệ số của hai vế, ta được:
\left\{ \begin{array}{l}
{K_1} + 1 = 200\\
{K_2} + 5 = 60\\
{K_3} + 6 = 14
\end{array} \right.Giải hệ phương trình trên, ta được:
\left\{ \begin{array}{l}
{K_1} = 199\\
{K_2} = 55\\
{K_3} = 8
\end{array} \right.Vậy: K = [199 55 8].
Mô phỏng Matlab
Bên cạnh phương pháp tính toán thủ công, ta có thể sử dụng phần mềm Matlab để mô phỏng và tìm ma trận K.
- Lập trình *m:
num = 1;
den = [1 6 5 1];
[A, B, C, D] = tf2ss(num,den)
p = [-2+4i,-2-4i,-10];
K = place(A,B,p)
Hình 2. Kết quả khi mô phỏng trên Matlab.
2.2. Phương pháp Canonical
Giả sử các cực vòng kín mong muốn:
s = {\mu _1},s = {\mu _2},....s = {\mu _n}Đa thức đặc trưng mong muốn:
\left( {s - {\mu _1}} \right)\left( {s - {\mu _2}} \right)...\left( {s - {\mu _n}} \right) = {s^n} + {\alpha _1}{s^{n - 1}} + {\alpha _2}{s^{n - 2}} + ... + {\alpha _{n - 1}}s + {\alpha _n}Ma trận vận chuyển T:
T = M.W
Trong đó:
- M là ma trận điều khiển được:
M=\left[\begin{matrix}B&AB&A^2B&\begin{matrix}...&A^{n-1}B\\\end{matrix}\\\end{matrix}\right]- W là ma trận được xác định như sau:
W=\left[\begin{matrix}a_{n-1}&a_{n-2}&...&\begin{matrix}a_1&1\\\end{matrix}\\a_{n-2}&a_{n-3}&...&\begin{matrix}1&0\\\end{matrix}\\...&...&...&\begin{matrix}...&...\\\end{matrix}\\\begin{matrix}a_1\\1\\\end{matrix}&\begin{matrix}1\\0\\\end{matrix}&\begin{matrix}...\\0\\\end{matrix}&\begin{matrix}\begin{matrix}0\\0\\\end{matrix}&\begin{matrix}0\\0\\\end{matrix}\\\end{matrix}\\\end{matrix}\right]Với ai là các hệ số của đa thức đặc trưng:
\left| {sI - A} \right| = {s^n} + {a_1}{s^{n - 1}} + {a_2}{s^{n - 2}} + ... + {a_{n - 1}}s + {a_n}Ma trận K:
K=\left[\begin{matrix}\alpha_n-a_n&\alpha_{n-1}-a_{n-1}&...&\alpha_1-a_1\\\end{matrix}\right].T^{-1}Để thực hiện phương pháp này, ta làm theo các bước sau đây:
- Bước 01 : Tìm đa thức đặc trưng và đa thức đặc trưng mong muốn từ đó suy ra: a1, a2,…, α1, α2,…, αn.
- Bước 02: Từ các ma trận của phương trình trạng thái và ai ta tìm được ma trận chuyển T, T-1.
- Bước 03: Dựa vào công thức tìm được ma trận K.
Ví dụ 2: Cho đối tượng có hàm truyền sau, hãy xác định ma trận hồi tiếp trạng thái K sao cho phương trình đặc tính có nghiệm tại vị trí mong muốn để đảm bảo chất lượng điều khiển của hệ thống:
\frac{{Y\left( s \right)}}{{U\left( s \right)}} = \frac{1}{{{s^3} + 6{s^2} + 5s + 1}}Hướng dẫn:
Các ma trận của phương trình trạng thái:
A=\left[\begin{matrix}0&1&0\\0&0&1\\-1&-5&-6\\\end{matrix}\right];B=\left[\begin{matrix}0\\0\\1\\\end{matrix}\right];C=\left[\begin{matrix}1&0&0\\\end{matrix}\right];D=0Chọn cực cho hệ kín: -2 ± j.4; -10.
Đa thức đặc trưng của hệ thống:
\left|sI-A\right|=\left|\left[\begin{matrix}s&0&0\\0&s&0\\0&0&s\\\end{matrix}\right]-\left[\begin{matrix}0&1&0\\0&0&1\\-1&-5&-6\\\end{matrix}\right]\right|=s^3+6s^2+5s+1Đồng nhất biểu thức, ta tìm được: a1 = 6; a2 = 5; a3 = 1.
Các ma trận của phương trình trạng thái:
M=\left[\begin{matrix}B&AB&A^2B\\\end{matrix}\right]=\left[\begin{matrix}0&0&1\\0&1&-6\\1&-6&31\\\end{matrix}\right]Chọn cực cho hệ kín:
W=\left[\begin{matrix}5&6&1\\6&1&0\\1&0&0\\\end{matrix}\right]Ma trận chuyển T:
T=M.W=\left[\begin{matrix}0&0&1\\0&1&-6\\1&-6&31\\\end{matrix}\right]\left[\begin{matrix}5&6&1\\6&1&0\\1&0&0\\\end{matrix}\right]=\left[\begin{matrix}1&0&0\\0&1&0\\0&0&1\\\end{matrix}\right]Suy ra:
T^{-1}=\left[\begin{matrix}1&0&0\\0&1&0\\0&0&1\\\end{matrix}\right]Đa thức đặc trưng mong muốn của hệ thống:
\begin{matrix}\left(s-\left(-2+j4\right)\right)\left(s-\left(-2-j4\right)\right)\left(s-\left(-10\right)\right)=s^3+14s^2+60s+200\\\Rightarrow\alpha_1=14,\alpha_2=60,\alpha_3=200\\\end{matrix}Ma trận K:
\begin{matrix}K=\left[\begin{matrix}\alpha_n-a_n&\alpha_{n-1}-a_{n-1}&...&\alpha_1-a_1\\\end{matrix}\right].T^{-1}\\K=\left[\begin{matrix}200-1&60-5&14-6\\\end{matrix}\right].\left[\begin{matrix}1&0&0\\0&1&0\\0&0&1\\\end{matrix}\right]\\K=\left[\begin{matrix}199&55&8\\\end{matrix}\right]\\\end{matrix}2.3. Phương pháp Ackermann
Để thực hiện phương pháp này, ta làm theo các bước sau đây:
- Bước 01: Tìm đa thức đặc tính mong muốn.
\det \left( {sI - A + BK} \right) = \left( {s - {p_1}} \right)\left( {s - {p_2}} \right)...\left( {s - {p_n}} \right)- Bước 02: Tìm φ(A) với ma trận A thay cho biến s ở trên.
- Bước 03: Tính K theo công thức:
K=\left[\begin{matrix}0&...&1\\\end{matrix}\right].M^{-1}.\varphi\left(A\right)Ví dụ 3: Cho đối tượng có hàm truyền sau, hãy xác định ma trận hồi tiếp trạng thái K sao cho phương trình đặc tính có nghiệm tại vị trí mong muốn để đảm bảo chất lượng điều khiển của hệ thống:
\frac{{Y\left( s \right)}}{{U\left( s \right)}} = \frac{1}{{{s^3} + 6{s^2} + 5s + 1}}Hướng dẫn:
Ta thành lập phương trình trạng thái dạng chính tắc điều khiển:
A=\left[\begin{matrix}0&1&0\\0&0&1\\-1&-5&-6\\\end{matrix}\right];B=\left[\begin{matrix}0\\0\\1\\\end{matrix}\right];C=\left[\begin{matrix}1&0&0\\\end{matrix}\right];D=0Chọn cực hệ kín là: -2 ± j.4; -10.
Đa thức đặc tính:
\det \left( {sI - A + BK} \right) = \left( {s + 2 + j4} \right)\left( {s + 2 - j4} \right)\left( {s + 10} \right) = {s^3} + 14{s^2} + 60s + 200Xét tính điều khiển được:
M=\left[\begin{matrix}B&AB&A^2B\\\end{matrix}\right]=\left[\begin{matrix}0&0&1\\0&1&-6\\1&-6&31\\\end{matrix}\right]Vì det(M) = -1, nên hệ thống điều khiển được.
Ta có:
\varphi\left(A\right)=A^3+14A^2+60A+200I=\left[\begin{matrix}199&55&8\\-8&159&7\\-7&-43&117\\\end{matrix}\right]Ma trận K:
K=\left[\begin{matrix}0&0&1\\\end{matrix}\right]\left[\begin{matrix}0&0&1\\0&1&-6\\1&-6&31\\\end{matrix}\right]^{-1}\left[\begin{matrix}199&55&8\\-8&159&7\\-7&-43&117\\\end{matrix}\right]Vậy: K = [199 55 8].
Mô phỏng Matlab:
Bên cạnh phương pháp tính toán thủ công, ta có thể sử dụng phần mềm Matlab để mô phỏng và tìm ma trận K.
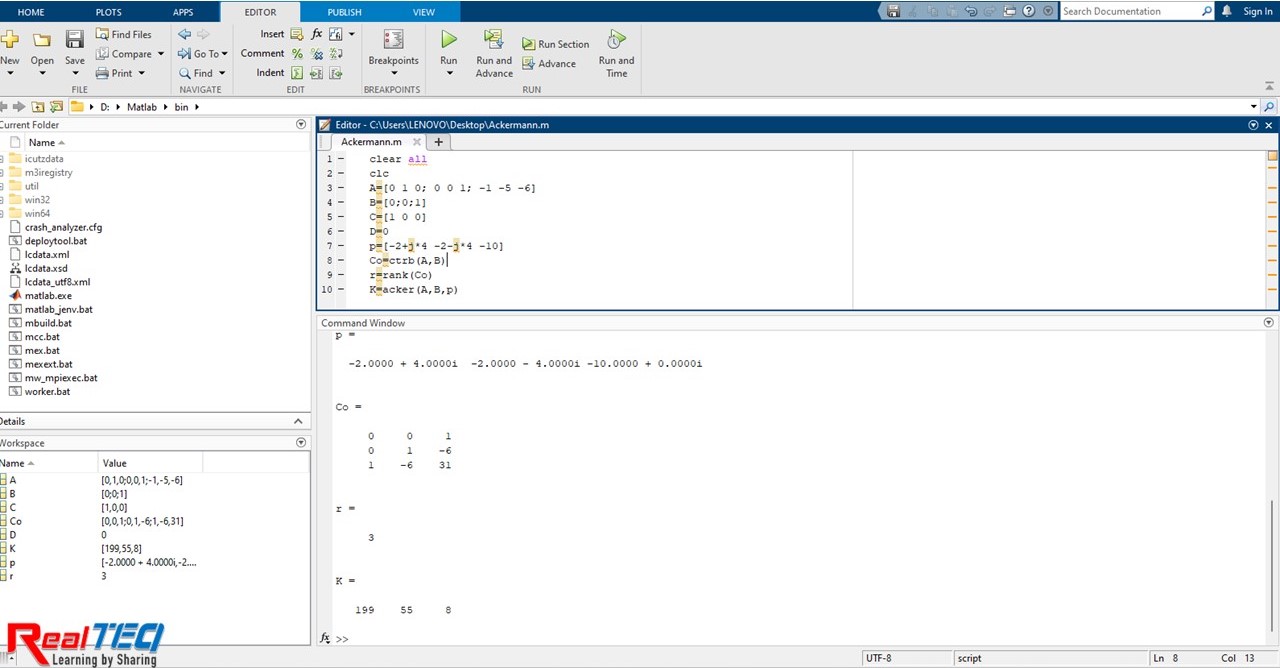
- Lập trình *m:
A=[0 1 0; 0 0 1; -1 -5 -6];
B=[0;0;1];
C=[1 0 0];
D=0;
p=[-2+j*4 -2-j*4 -10];
Co=ctrb(A,B)
r=rank(Co)
K=acker(A,B,p)
Hình 3. Kết quả khi mô phỏng trên Matlab.
 Real Group Efficiency Projects
Real Group Efficiency Projects