1. Bộ điều khiển PID là gì?
Một cách đơn giản nhất để hiểu về PID như sau:
- P: là phương pháp điều chỉnh tỉ lệ, giúp tạo ra tín hiệu điều chỉnh tỉ lệ với sai lệch đầu vào theo thời gian lấy mẫu.
- I: là tích phân của sai lệch theo thời gian lấy mẫu. Điều khiển tích phân là phương pháp điều chỉnh để tạo ra các tín hiệu điều chỉnh sao cho độ sai lệch giảm về 0. Từ đó cho ta biết tổng sai số tức thời theo thời gian hay sai số tích lũy trong quá khứ. Khi thời gian càng nhỏ thể hiện tác động điều chỉnh tích phân càng mạnh, tương ứng với độ lệch càng nhỏ.
- D: là vi phân của sai lệch. Điều khiển vi phân tạo ra tín hiệu điều chỉnh sao cho tỉ lệ với tốc độ thay đổi sai lệch đầu vào. Thời gian càng lớn thì phạm vi điều chỉnh vi phân càng mạnh, tương ứng với bộ điều chỉnh đáp ứng với thay đổi đầu vào càng nhanh.
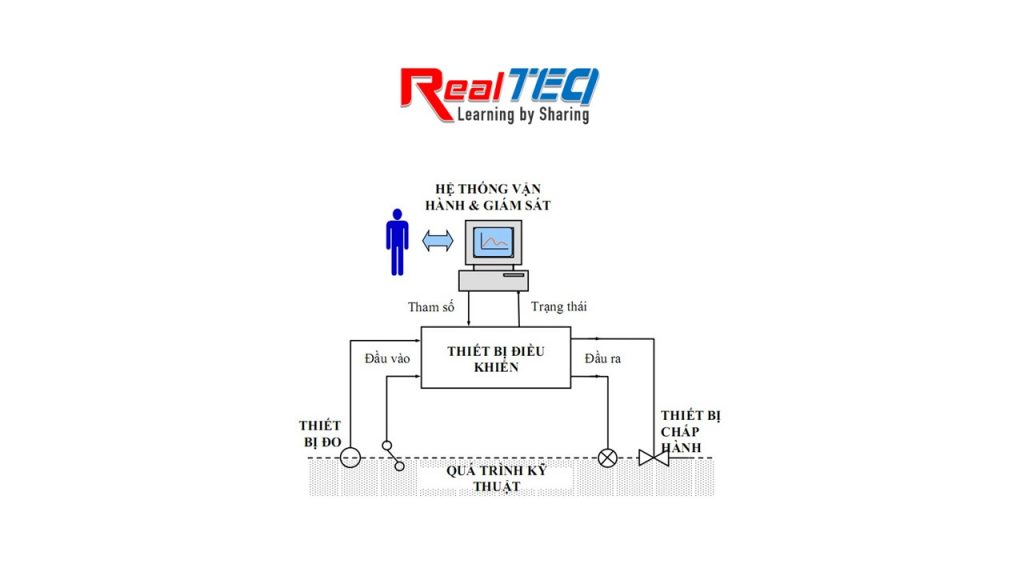
Một bộ điều khiển vi tích phân tỉ lệ (PID- Proportional Integral Derivative) là một cơ chế phản hồi vòng điều khiển được sử dụng rộng rãi trong các hệ thống điều khiển công nghiệp – bộ điều khiển PID là bộ điều khiển được sử dụng nhiều nhất trong các bộ điều khiển phản hồi. Bộ điều khiển PID sẽ tính toán giá trị “sai số” là hiệu số giữa giá trị đo thông số biến đổi và giá trị đặt mong muốn. Bộ điều khiển sẽ thực hiện giảm tối đa sai số bằng cách điều chỉnh giá trị điều khiển đầu vào.
Hình 1. Cấu trúc của hệ thống điều khiển PID.
Trong trường hợp không có kiến thức cơ bản (mô hình toán học) về hệ thống điều khiển thì bộ điều khiển PID là sẽ bộ điều khiển tốt nhất. Tuy nhiên, để đạt được kết quả tốt nhất, các thông số PID sử dụng trong tính toán phải điều chỉnh theo tính chất của hệ thống-trong khi kiểu điều khiển là giống nhau, các thông số phải phụ thuộc vào đặc thù của hệ thống.
Hình 2. Hệ thống điều khiển nhiệt độ sử dụng PID.
2. Mục đích sử dụng bộ điều khiển PID
PID được coi là bộ điều khiển lý tưởng của các hệ thống điều khiển quy trình hiện đại. Nó được sử dụng hầu hết trong các ứng dụng điều khiển quá trình tự động trong công nghiệp hiện nay. Để điều chỉnh lưu lượng, nhiệt độ, áp suất,…
- Giảm sai số xác lập đến mức tối thiểu nhất
- Hạn chế độ dao động
- Giảm thời gian xác lập và độ vọt lố.
3. Các thuật toán và thống số của điều khiển PID
3.1. Khâu tỉ lệ
Khâu tỉ lệ (đôi khi còn được gọi là độ lợi) làm thay đổi giá trị đầu ra, tỉ lệ với giá trị sai số hiện tại. Đáp ứng tỉ lệ có thể được điều chỉnh bằng cách nhân sai số đó với một hằng số Kp, được gọi là hệ số tỉ lệ.
Khâu tỉ lệ được cho bởi:
Pout = Kp.e(t)
Trong đó
- Pout: thừa số tỉ lệ của đầu ra.
- Kp: Hệ số tỉ lệ, thông số điều chỉnh.
- e: sai số.
- t: thời gian hay thời gian tức thời (hiện tại).
Hệ số của khâu tỉ lệ lớn là do thay đổi lớn ở đầu ra mà sai số thay đổi nhỏ. Nếu hệ số của khâu tỉ lệ quá cao, hệ thống sẽ không ổn định. Ngược lại, hệ số nhỏ là do đáp ứng đầu ra nhỏ trong khi sai số đầu vào lớn, và làm cho bộ điều khiển kém nhạy, hoặc đáp ứng chậm. Nếu Hệ số của khâu tỉ lệ quá thấp, tác động điều khiển có thể sẽ quá bé khi đáp ứng với các nhiễu của hệ thống.
Để chúng ta có thể hiểu rõ hơn thì bây giờ cũng nhau xét một ví dụ cụ thể như sau: Có một chiếc xe hơi đang ở vị trí A và ta muốn di chuyển tới vị trí B, biết rằng khoảng cách từ A đến B là 50m.
Chúng ta có thể mô hình hóa về dạng sơ đồ khối với vị trí 50m là vị trí mong muốn. Ta thử sử dụng phương pháp điều khiển tỉ lệ P với Kp = 0,1 cho mô hình này và xem điều gì sẽ xảy ra?
Hình 3. Mô hình hệ thống khi xe hơi ở vị trí ban đầu.
Đầu tiên, ta thấy khi ở vị trí ban đầu, sai số lúc này sẽ là là 50m, khi qua bộ điều khiển P thì tốc độ sẽ là 5m/s tác động vào chiếc xe di chuyển, khi xe di chuyển thì vị trí sẽ tăng dần (đồng nghĩa với việc sai số sẽ giảm xuống). Giả sử lúc này vị trí xe đang ở 10m thì sai số sẽ là 40, tốc độ của xe giảm xuống còn 4m/s. Cứ như vậy vị trí xe tăng dần lên và khoảng cách cũng sẽ giảm dần về 0, khi về 0 xe sẽ dừng hẳn ở vị trí 50m. Vậy nếu xe vượt quá vị trí 50m do quán tính thì sẽ như thế nào? Chúng ta có thể an tâm vì bộ điều khiển vẫn có thể hoạt động tốt trong trường hợp này. Khi có vọt lố xảy ra, đầu ra của bộ điều khiển sẽ có giá trị âm và điều khiển xe chạy với vận tốc âm (nghĩa là cho xe lùi lại) để có thể về với vị trí mong muốn 50m.
Hình 4. Mô hình hệ thống khi xe hơi ở vị trí 60m.
Như vậy với ví dụ này ta có thể nhận xét được giá trị Kp càng lớn thì tốc độ của xe sẽ càng lớn và càng nhanh chạm đến được vị trí mong muốn. Nhưng nếu giá trị Kp không phù hợp thì độ vọt lố tăng cao và có thể dẫn đến mất ổn định cho hệ thống.
Hình 5. Đồ thị vị trí của xe hơi với các giá trị Kp khác nhau.
Bộ điều khiển tỉ lệ P hoạt động rất tốt với ví dụ trên, nhưng bây giờ hãy xét ví dụ tiếp theo xem nó có hoạt động tốt như vậy nữa hay không? Bây giờ chúng ta có một chiếc máy bay trực thăng và muốn nó bay lơ lửng ở độ bao 50m (giả sử để máy bay có thể lơ lửng thì tốc độ cánh quạt phải là 1000 vòng/phút).
Hình 6. Trực thăng đang ở trên mặt đất.
Cũng giống như ví dụ trước, ta sẽ cho giá trị Kp ban đầu bằng 20 và xét điều gì sẽ xảy ra?
Hình 7. Mô hình hệ thống khi trực thăng ở trên mặt đất và Kp = 20.
Lúc này cánh quạt quay với tốc độ 1000 vòng/phút và tất nhiên nó chỉ có thể xê dịch qua lại trên mặt đất mà không bay lên được. Vậy giá trị Kp không phù hợp. Hãy thử tăng giá trị Kp lên 50 và tiếp tục quan sát.
Hình 8. Mô hình hệ thống khi trực thăng ở trên mặt đất và Kp = 50.
Ban đầu trực thăng sẽ bay lên vì vận tốc cánh quạt lúc này là 2500 vòng/phút. Khi trực thăng càng bay cao lên thì sai số sẽ giảm đi và tốc độ cũng giảm xuống. Điều đặc biệt là khi đạt tới độ cao 20m thì trực thăng sẽ lơ lửng mà không thể bay lên cao nữa vì tốc độ cánh quạt tại độ cao này là 1000 vòng/phút. Như vậy ta tiếp tục tăng giá trị Kp lên và có được bảng các sai số khi thay đổi các giá trị Kp như sau:
|
Giá trị Kp |
Sai số (m) |
|
20 |
50 |
|
50 |
20 |
|
100 |
10 |
|
1000 |
1 |
Từ bảng sai số ta thấy rằng nếu muốn sai số càng nhỏ thì ta phải tăng giá trị Kp càng lớn. Nhưng sai số này chỉ có thể nhỏ đi mà không thể nào có thể bằng không được hoặc nói cách khác là hệ thống này luôn luôn tồn tại sai số, sai số này gọi là sai số xác lập. Mặt khác khi ta tăng giá trị Kp quá lớn, không phù hợp sẽ làm cho hệ thống mất ổn định.
Hình 9. Sai số xác lập của hệ thống.
Vậy thì làm thế nào để có thể triệt tiêu sai số xác lập này? Khâu tích phân I sẽ giúp chúng ta làm việc này.
3.2. Khâu tích phân
Phân phối của khâu tích phân (đôi khi còn gọi là reset) tỉ lệ thuận với cả biên độ sai số lẫn quãng thời gian xảy ra sai số. Tổng sai số tức thời theo thời gian (tích phân sai số) cho ta tích lũy bù đã được hiệu chỉnh trước đó. Tích lũy sai số sau đó được nhân với độ lợi tích phân và cộng với tín hiệu đầu ra của bộ điều khiển. Biên độ phân phối của khâu tích phân trên tất cả tác động điều chỉnh được xác định bởi độ lợi tích phân.
Thừa số tích phân được cho bởi:
{I_{out}} = {K_i}\int\limits_0^t {e\left( \tau \right)} .d\tauTrong đó
- Iout: thừa số tích phân của đầu ra
- Ki: độ lợi tích phân, 1 thông số điều chỉnh
- e: sai số = SP-PV
- t: thời gian hoặc thời gian tức thời (hiện tại)
- t : một biến tích phân trung gian
Khâu tích phân (khi cộng thêm khâu tỉ lệ) sẽ tăng tốc chuyển động của quá trình tới điểm đặt và khử số dư sai số ổn định với một tỉ lệ chỉ phụ thuộc vào bộ điều khiển. Tuy nhiên, vì khâu tích phân là đáp ứng của sai số tích lũy trong quá khứ, nó có thể khiến giá trị hiện tại vọt lố qua giá trị đặt (ngang qua điểm đặt và tạo ra một độ lệch với các hướng khác). Để tìm hiểu thêm các đặc điểm của việc điều chỉnh độ lợi tích phân và độ ổn của bộ điều khiển.
Tiếp tục với ví dụ trực thăng ở trên, bây giờ ta sẽ đặt vào song song với khối tỉ lệ P một khối tích phân I và xem các nó hoạt động.
Hình 10. Mô hình hệ thống trực thăng khi có thêm khối tích phân I và đồ thị sai số hệ thống.
Ta có thể dễ dàng thấy rằng giá trị tích phân của hàm sai số này sẽ tăng theo thời gian vì khi ở trại tháng xác lập, sai số là một hằng số lớn hơn 0. Nói cách khác lỗi càng lớn và thời gian lỗi càng lâu thì giá trị tích phân của hàm sai số sẽ càng lớn.
Hình 11. Mối tương quan của đầu vào và đầu ra của khối tích phân I và độ vọt lố của hệ thống.
Như vậy, nếu hệ thống có sai số xác lập thì giá trị I sẽ tăng lên, điều này đồng nghĩa với việc V (tốc độ cánh quạt) cũng sẽ tăng lên làm cho trực thăng tiến tới độ cao mong muốn là 50m. Khi đạt tới độ cao mong muốn thì lúc này giá trị I sẽ không còn tăng lên nữa (vì sai số đã bị triệt tiêu).
Điều này có vẻ hoàn hảo, nhưng trong thực tế, giá trị V có thể sẽ tăng rất cao (vì sai số quá lớn) làm cho trực thăng bay lên cao hơn độ cao mong muốn (độ vọt lố) và có thể làm cho hệ thống mất tính ổn định.
Khâu vi phân (đạo hàm) sẽ giúp chúng ta có thể khắc phục được độ vọt lố này.
3.3. Khâu vi phân
Tốc độ thay đổi của sai số quá trình được tính toán bằng cách xác định độ dốc của sai số theo thời gian (tức là đạo hàm bậc một theo thời gian) và nhân tốc độ này với độ lợi tỉ lệ Kd. Biên độ của phân phối khâu vi phân (đôi khi được gọi là tốc độ) trên tất cả các hành vi điều khiển được giới hạn bởi độ lợi vi phân, Kd.
Thừa số vi phân được cho bởi:
{D_{out}} = {K_d}.\frac{{d.e\left( t \right)}}{{dt}}Trong đó
- Dout: thừa số vi phân của đầu ra.
- Kd: Độ lợi vi phân, một thông số điều chỉnh.
- e: Sai số = SP-PV.
- t :thời gian hoặc thời gian tức thời (hiện tại).
Khâu vi phân làm chậm tốc độ thay đổi của đầu ra bộ điều khiển và đặc tính này là đang chú ý nhất để đạt tới điểm đặt của bộ điều khiển. Từ đó, điều khiển vi phân được sử dụng để làm giảm biên độ vọt lố được tạo ra bởi thành phần tích phân và tăng cường độ ổn định của bộ điều khiển hỗn hợp. Tuy nhiên, phép vi phân của một tín hiệu sẽ khuếch đại nhiễu và do đó khâu này sẽ nhạy hơn đối với nhiễu trong sai số, và có thể khiến quá trình trở nên không ổn định nếu nhiễu và độ lợi vi phân đủ lớn. Do đó một xấp xỉ của bộ vi sai với băng thông giới hạn thường được sử dụng hơn. Chẳng hạn như mạch bù sớm pha.
Nhưng chúng ta đã biết thì vi phân sẽ giúp chúng ta biết được tốc độ thay đổi của một hàm số tại thời điểm nhất định nào đó.
Ở đây tốc độ thay đổi càng lớn thì giá trị vi phân của sai số đó càng lớn.
Hình 12. Mối tương quan giữa đầu vào và đầu ra của khối vi phân D.
Cũng với ví dụ về trực thăng ở trên, ta cũng đặt vào song song một khối vi phân D.
Hình 13. Mô hình và đồ thị của hệ thống khi có bộ điều khiển PID.
Ở ví dụ này ta có thể hiểu một cách đơn giản rằng, khi trực tăng bay lên một cách nhanh chóng (tốc độ cánh quạt cao, sai số giảm nhanh) do giá trị I và P lớn thì khâu vi phân sẽ đưa ra giá trị D bé hơn 0 làm giảm giá trị V để trực thăng giảm tốc độ tiến đến độ cao mong muốn (tránh vọt lố). Trong trường hợp xảy ra vọt lố mà không có khâu vi phân thì lúc này giá trị P sẽ âm, làm tốc độ cánh quạt giảm một cách đột ngột, trực thăng sẽ bị rơi tự do. Vậy nên khi xảy vọt lố và có khâu vi phân, giá trị D sẽ dương, tốc độ rơi của trực thăng càng lớn (sai số tiến về 0 càng nhanh) thì D sẽ càng lớn và ngược lại. Điều này làm cho trực thăng có thể tiến tới độ cao 50m một cách chính xác nhất.
Khi có cả ba khâu P, I và D thì giá trị V (tốc độ của cánh quạt) sẽ được điều chỉnh một cách tốt nhất để đạt được độ cao 50m.
4. Các loại điều khiển
- Bộ điều khiển tỉ lệ – P (Proportional Controller).
- PI (Proportinal and Integral Controller) gọi là bộ điều khiển tỉ lệ và tích phân.
- PD (Proportional and Derivative (PD) Controller) gọi là bộ điều khiển đạo hàm.
- PID (Proportional, Integral, and Derivative (PID) Controller) là bộ điều khiển tỉ lệ – tích phân – đạo hàm (vi phân).
Vài ứng dụng có thể yêu cầu chỉ sử dụng một hoặc hai khâu tùy theo hệ thống. Điều này đạt được bằng cách thiết đặt đội lợi của các đầu ra không mong muốn về 0. Một bộ điều khiển PID sẽ được gọi là bộ điều khiển PI, PD, P hoặc I nếu vắng mặt các tác động bị khuyết. Bộ điều khiển PI khá phổ biến, do đáp ứng vi phân khá nhạy đối với các nhiễu đo lường, trái lại nếu thiếu giá trị tích phân có thể khiến hệ thống không đạt được giá trị mong muốn.
5. Ví dụ minh họa
Đề bài: Sử dụng phương pháp Ziegler Nichols để thiết kế bộ điều khiển PID cho hệ thống có hàm truyên và đáp ứng như bên dưới. Biết T1 = 9, T2 = 141, K = 0,75.
G\left( s \right) = \frac{{0,75.{e^{ - 1,21s}}}}{{\left( {30s + 1} \right)\left( {5s + 1} \right)\left( {2s + 1} \right)}}Hình 14. Đáp ứng đầu ra của hệ thống.
- Sử dụng matlab lập trình để tìm hàm truyền của bộ điều khiển PID:
Hình 15. Lập trình m file (*.m).
- Sử dụng simulink để mô phỏng hệ thống:
Hình 16. Đáp ứng đầu ra của hệ thống khi chưa có bộ điều khiển PID.
Hình 17. Đáp ứng đầu ra của hệ thống sau khi dử dụng bộ điều khiển PID.
Nhận xét:
- Ta thấy rằng hệ thống trước khi sử dụng bộ điều khiển PID thì đáp ứng đầu ra của hệ thống không thể đặt đến giá trị mong muốn là 1 mà chúng ta đưa vào lúc ban đầu của hệ thống, và sau khi sử dụng bộ điều khiển PID thì đầu ra của hệ thống đã đạt đến được giá trị mong muốn ở đầu vào.
- Nhưng có một lưu ý nhỏ khi sử dụng bộ điều khiển PID thì hệ thống đã có vọt lố và giao động. Vì đây là bài tính toán và mô phỏng bằng phần mềm nên sẽ có một ít sai lệch của sai số và bộ điều khiển cũng chưa ở dạng tốt nhất.
- Cho nên khi chúng ta tính toán thông số của bộ điều khiển PID thì chúng ta nên tăng giảm các thông số của bộ điều khiển một cách hợp lí để cho đáp ứng đầu ra của hệ thống là tốt nhất.